Matematica I: Exponentes y Radicales

¿Que es un exponente?

El exponente de un número nos dice cuantas veces se usa el numero en una multiplicación

Ej: 8² = 8 × 8 = 64 .

*Leyes de los exponentes

Las tres primeras leyes (x¹ = x, x⁰ = 1 y x^-1 = 1/x) son sólo parte de la sucesión natural de exponentes.

La ley que dice que x^mxⁿ = x^m+n

En x^mxⁿ, ¿cuántas veces multiplicas "x"? Respuesta: primero "m" veces, después otras "n" veces, en total "m+n" veces.

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

Así que x²x³ = x⁽²⁺³⁾ = x⁵

La ley que dice que x^m/xⁿ = x^m-n

Como en el ejemplo anterior, ¿cuántas veces multiplicas "x"? Respuesta: "m" veces, después reduce eso "n" veces (porque estás dividiendo), en total "m-n" veces.

Ejemplo: x^4-2 = x⁴/x² = (xxxx) / (xx) = xx = x²

(Recuerda que x/x = 1, así que cada vez que hay una x "sobre la línea" y una "bajo la línea" puedes cancelarlas.)

Esta ley también te muestra por qué x⁰=1 :

Ejemplo: x²/x² = x^2-2 = x⁰ =1

La ley que dice que (x^m)ⁿ = x^mn

Primero multiplicas x "m" veces. Después tienes que hacer eso "n" veces, en total m×n veces.

Ejemplo: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

Así que (x³)⁴ = x^3×4 = x¹²

La ley que dice que (xy)ⁿ = xⁿyⁿ

Para ver cómo funciona, sólo piensa en ordenar las "x"s y las "y"s como en este ejemplo:

Ejemplo: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

La ley que dice que (x/y)ⁿ = xⁿ/yⁿ

Parecido al ejemplo anterior, sólo ordena las "x"s y las "y"s

Ejemplo: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

La ley que dice que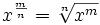

Para entenderlo, sólo recuerda de las fracciones que n/m = n × (1/m):

Ejemplo: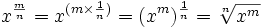

¿Qué pasa si el exponente es 1 o 0?

Si el exponente es 1, entonces tienes el número solo (por ejemplo 9¹ = 9)

Si el exponente es 0, la respuesta es 1 (por ejemplo 9⁰ = 1)

El extraño caso de 0⁰

Hay dos argumentos diferentes sobre el valor correcto. 0⁰ podría ser 1, o quizás 0, así que alguna gente dice que es "indeterminado":

	x⁰ = 1, así que ...	0⁰ = 1
	0ⁿ = 0, así que ...	0⁰ = 0
	Cuando dudes...	0⁰ = "indeterminado"

Exponentes fraccionarios

$Resultado de imagen para exponente fraccionario ejercicios$

También se llaman "radicales"

¿Que es un radical ?

Cuando no puedes simplificar un número para quitar una raíz cuadrada (o una raíz cúbica, etc.) entonces es un radical.

Un radical es equivalente a una potencia de exponente fraccionario en la que el denominador de la fracción es el índice del radical y el numerador de la fracción es el exponente del radicando.

propiedades delos radicales

1- ) Raíz de un producto: La raíz de un producto es igual al producto de las raíces de los factores nombrados anteriormente.

$\sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}$

Ej: $\sqrt{3^2 \cdot 2^4}$ = $\sqrt{3^2} \cdot \sqrt{2^4}$ = $\sqrt{9} \cdot \sqrt{16} = 3\cdot 4 = 12.$

Se llega a igual resultado de la siguiente manera:

$\sqrt{3^2 \cdot 2^4} = \sqrt{9 \cdot 16} = \sqrt{144} = 12.$

2- ) Raíz de un cociente: La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador.

$\sqrt[n]{\frac{a}{b}} = \frac{a^{1/n}}{b^{1/n}}$ = $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

Ejemplo

$\sqrt{\frac{9}{4}} = \frac{\sqrt{9}}{\sqrt{4}}$ = $\frac{3}{2}.$

3- ) Raíz de una raíz: Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando.

$\sqrt[n]{\sqrt[m]{a}}$ = $\sqrt[n \cdot m]{a}.$

Ejemplo

$\sqrt[9]{\sqrt[3]{5}}$ = $\sqrt[27]{5}.$

4- ) Potencia de una raíz: Para calcular la potencia de una raíz se eleva el radicando a esa potencia.

$\left(\sqrt[n]{a} \right)^m =\sqrt[n]{a^m} = a^{\frac{m}{n}}$

Ejemplo

si 3 y 4

$\left(\sqrt[4]{x} \right)^3 = \sqrt[4]{x^3}$ = $\ x^{\frac{3}{4}}.$

5- ) Potencia de un producto: La raíz de un producto con el mismo radicando y distintos índices, que se obtiene multiplicando los índices de las raíces y conservando el radicando elevado a la suma de los índices.

$\sqrt[m]{a} \cdot \sqrt[n]{a} = a^{\frac{1}{m}+\frac{1}{n}} = a^{\frac{m+n}{mn}} = \sqrt[m \cdot n]{{a}^{m +n}}$

Matematica I

lunes, 27 de febrero de 2017

Exponentes y Radicales

La ley que dice que x^mxⁿ = x^m+n

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

La ley que dice que x^m/xⁿ = x^m-n